
We're highlighted in Edutopia again—this time for how well our authentic tasks promote productive math struggle.

Raise your hand if you've ever heard a student say, I hate math. Why is it that some students don't like going to math class? Is there something we can do to change their mindset about mathematics?

Math Exemplars work to develop the whole child in mathematics and social-emotional learning.
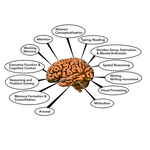
To help your students achieve indelible long-term learning, let’s use the latest in brain research to their advantage.

It is a new year with new students and new problems to solve! There is nothing like having the opportunity to start the year off fresh. My number one goal in the very beginning is to help students fall in love with solving problems.

When you walk into my classroom, you might be taken aback by the noise level. But don't worry, it's intentional.

What do we hope to help our math students become? I bet your answer includes, “learners who are ready to use their math skills in the real world to solve real-world problems.”

So why did the vast majority of American students struggle on the NAEP? In order to find an answer to this question, I decided to take the NAEP tests myself.

Encouraging students to work together can lead to deeper understanding for all students, and in turn boost mathematical achievement.

From jotting down informal ideas to creating a persuasive formal piece, bringing writing into your science teaching will help your students analyze the concepts further, and can lead to the discovery of new knowledge, connections, and ideas.

We're kicking off 5 Days of Exemplars, a series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. You’ll discover new ideas you can use right away!

How can we get our students genuinely excited about science? It’s a question that so many of us are looking for the answer to. So we’ve started something fun to help: Science Talk!
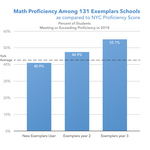
Over the last two years, COVID-19 has disrupted every aspect of our lives—including the momentum young learners need for growth. Read on to discover effective ways to support learning recovery with Exemplars.

We've created a tool you can use to seamlessly weave SEL practices into your Exemplars lessons. Aligned to our Problem-Solving Process, this resource suggests routines for each step along the way.

This new mathematical formula interconnects Exemplars problem-solving tasks and the CASEL framework. The agendas of both the CASEL and Exemplars pedagogies strive to create classroom cultures that are heavily student-focused and driven by personal growth.

How do we prepare our students for end-of-year performance tasks on statewide tests while—at the same time—ensure that we are utilizing the precious minutes in every class period and are not “teaching to the tests?”

As schools and districts across the country begin to think about how to re-engage students in learning, consider science as a place to begin. Why science? Because science is naturally engaging for students.

Stress has a serious impact on how students learn. Read on to discover some science-based reasons for making fun a priority, and how to do it without losing sight of your curricular goals.

In order to support a talk rich classroom, I need to feed the learning. The Exemplars problems are rich and engaging tasks that my students eagerly unpack. With each new unit of study, I follow an instructional routine that allows students to acquire knowledge and skills in a predictable manner.

As we prepare to welcome our students back, let’s remember that the best learning truly is a community activity.
This is the start of a strong solution. Welcome to day one of our deep dive into how to help students grow into capable, confident problem solvers. For students to realize the full benefits of authentic problem-solving tasks, you need strategies to help them successfully read and unpack these rigorous problems. Read on for effective strategies.

Students enjoy thinking for themselves—they need your support, but not too much! So how do you offer just the right guidance and ask just enough questions without inadvertently “stealing” their opportunity to solve the problem on their own and the thrill of discovery that will keep them engaged through a challenge?

Once you've prepared your students with a solid understanding of complex performance tasks ... and once you've guided them as s they select a strategy for solving it ... what's your role–and what's your goal–as they work to find solutions? Check out these best practices.
Your students can find an answer. But can they create solutions? The difference between a simple answer–a simple computation, for example–and a rich mathematical solution that demonstrates the depth of their understanding is vast. Learn about a simple framework that supports students in developing persuasive solutions.
When students assess their own work at the end of a task they not only discover how to improve their solutions, but they build skills that will empower them throughout their problem-solving lives. Learn how to apply self- and peer-assessment practices in your classroom to boost key critical thinking and reasoning skills.
Teachers need technologies that provide students with a virtual “math playground” to explore, discover, and create. That’s why Exemplars is so excited to be partnering with Brainingcamp! As part of a special offer, Brainingcamp provides free trials and can extend a 15% discount to all Exemplars Math Library subscribers.
The Three Reads Protocol is one way to do a close read of a complex math task. This strategy includes reading a math scenario three times with a different goal each time. This blog offers tips and suggestions for how to adapt this method to a virtual learning environment.
Upon completing an Exemplars task, what should a student’s final problem-solving solution look like? In this video, we will walk students through what they should be thinking about and what they should include to create strong math solutions.

This video tutorial is designed specifically for kids to help them get started with our problem-solving process from home.

Take a deep breath! Your students do not need to be proficient tomorrow. As with anything new, it’s going to be best to use a model of gradual release as you introduce this to your students. There are several different ways you can approach this …
Our “problem-solving procedure” hits the news in Edutopia — and boosts math and reading scores!

We are pleased to announce that ReContext Data Solutions, LLC, an independent, outside research organization, has determined that Exemplars performance material in mathematics is “evidence-based” and meets ESSA’s Tier 3 standards.

We asked a powerhouse teaching team to share their Exemplars experience. In an inspirational conversation, a panel of educators at Brooklyn's PS 12 offered ten amazing ways that using Exemplars has transformed their school.
This blog represents part one of a four-part series that explores mathematical connections and offers guidelines, strategies and suggestions for helping teachers elicit this type of thinking from their students. We find many students enjoy making connections once they learn how to reflect and question effectively.

The math laboratory is in its second year at PS 54. Last year, our data saw increased math scores for the classes that participated in the problem-solving lab. This year, the trend continued and all general education students passed the state math exam.
The Exemplars Problem Solving Procedure has supported students in understanding a problem, identifying a strategy to use, solve the problem, communicate findings in words, and trying to solve a problem in another way.

Long gone are the days of the stand and deliver as an effective way to teach. Science instruction is now more about sense-making than memorization.

Time. It seems we never have enough time. Not enough time to teach everything we need to teach. And science is usually the subject most affected by this lack of time.

If our children understand the why and the how of science, technology, and engineering, they are better able to make informed decisions as part of a democratic society. In order for students to do this, they must regularly engage with, investigate, and explain scientific phenomena.

Promoting discourse from rich tasks that move mathematical thinking forward challenges elementary teacher candidates, as their past experiences in working with both mathematics and children is often limited.

Problem solving is a life-long skill all mathematicians use. The true power of a mathematician is the ability to see math in all situations and solve problems using a toolbox of proven strategies.

This blog features a few suggestions for getting started with Exemplars Science. There is no right or wrong way to begin. The important thing is to begin. Have fun with it!

Once upon a time, Americans might have been content to live in a community much like Garrison Keillor’s Lake Wobegon, “where all the children are above average.” That’s because historically American kids, and our schools, were above average; however, for decades, America’s education system has been losing ground internationally.

Dr. Brewer, founder of Exemplars, along with others, asked an important question, “How do we determine if students can utilize the mathematics they are learning in the classroom to address and solve the complex problems they eventually will be asked to address in the “real world?”

We're highlighted in Edutopia again—this time for how well our authentic tasks promote productive math struggle.

Raise your hand if you've ever heard a student say, I hate math. Why is it that some students don't like going to math class? Is there something we can do to change their mindset about mathematics?

Math Exemplars work to develop the whole child in mathematics and social-emotional learning.

To help your students achieve indelible long-term learning, let’s use the latest in brain research to their advantage.

It is a new year with new students and new problems to solve! There is nothing like having the opportunity to start the year off fresh. My number one goal in the very beginning is to help students fall in love with solving problems.

When you walk into my classroom, you might be taken aback by the noise level. But don't worry, it's intentional.

What do we hope to help our math students become? I bet your answer includes, “learners who are ready to use their math skills in the real world to solve real-world problems.”

So why did the vast majority of American students struggle on the NAEP? In order to find an answer to this question, I decided to take the NAEP tests myself.

Encouraging students to work together can lead to deeper understanding for all students, and in turn boost mathematical achievement.

We're kicking off 5 Days of Exemplars, a series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. You’ll discover new ideas you can use right away!

Why are the students so happy? I really wanted to know. So, I did what anyone would do: I went straight to the source and asked the kiddos. Here’s what I learned.

Over the last two years, COVID-19 has disrupted every aspect of our lives—including the momentum young learners need for growth. Read on to discover effective ways to support learning recovery with Exemplars.

Exemplars rich math tasks and Problem-Solving Process create the perfect setting for SEL growth and development.

A valuable approach for addressing COVID “learning gaps” is the utilization of expanded learning. Expanded school days, educational time before and after school, and summer schooling all multiply your students’ chance for success.

Don’t panic! “Acceleration” is less of a “hurry up” and more of a “ramping up.” We have instructional strategies that you can use to help these students catch up to their peers. It’s all about finding a pace and rigor that’s right for them.

Utilizing our highly potent program allows precious minutes in school tutoring sessions to be maximized for optimum learning outcomes.

We've created a tool you can use to seamlessly weave SEL practices into your Exemplars lessons. Aligned to our Problem-Solving Process, this resource suggests routines for each step along the way.

This new mathematical formula interconnects Exemplars problem-solving tasks and the CASEL framework. The agendas of both the CASEL and Exemplars pedagogies strive to create classroom cultures that are heavily student-focused and driven by personal growth.

How do we prepare our students for end-of-year performance tasks on statewide tests while—at the same time—ensure that we are utilizing the precious minutes in every class period and are not “teaching to the tests?”

Stress has a serious impact on how students learn. Read on to discover some science-based reasons for making fun a priority, and how to do it without losing sight of your curricular goals.

In order to support a talk rich classroom, I need to feed the learning. The Exemplars problems are rich and engaging tasks that my students eagerly unpack. With each new unit of study, I follow an instructional routine that allows students to acquire knowledge and skills in a predictable manner.

As we prepare to welcome our students back, let’s remember that the best learning truly is a community activity.

Exemplars problem-solving performance tasks offer a high-potency solution for any learning environment, bringing together the three most important subjects in primary education – reading, writing, and mathematics.

After 13 years in education, I have used Exemplars in different grade levels and various demographic and socioeconomic areas, but the results were always the same. The real-life connections, self-motivation to gain the desired level, and the critical higher-order reasoning that is expected both challenges and motivates all types of students.

Exemplars tasks provide a welcome contrast to the school district’s highly-structured and scripted base math program. It is through the Exemplars tasks that my students are freed to use their creativity and find their voices as young mathematicians

When my administration and fabulous PTA asked, “What supplemental resources will help you teach and reach the entire spectrum of your students?” of course I was the first one to say, “the Exemplars Program please!”
This is the start of a strong solution. Welcome to day one of our deep dive into how to help students grow into capable, confident problem solvers. For students to realize the full benefits of authentic problem-solving tasks, you need strategies to help them successfully read and unpack these rigorous problems. Read on for effective strategies.

Students enjoy thinking for themselves—they need your support, but not too much! So how do you offer just the right guidance and ask just enough questions without inadvertently “stealing” their opportunity to solve the problem on their own and the thrill of discovery that will keep them engaged through a challenge?

Once you've prepared your students with a solid understanding of complex performance tasks ... and once you've guided them as s they select a strategy for solving it ... what's your role–and what's your goal–as they work to find solutions? Check out these best practices.
Your students can find an answer. But can they create solutions? The difference between a simple answer–a simple computation, for example–and a rich mathematical solution that demonstrates the depth of their understanding is vast. Learn about a simple framework that supports students in developing persuasive solutions.
When students assess their own work at the end of a task they not only discover how to improve their solutions, but they build skills that will empower them throughout their problem-solving lives. Learn how to apply self- and peer-assessment practices in your classroom to boost key critical thinking and reasoning skills.

We’re sharing 5 Days of Exemplars, a blog series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. Read on to learn more.
In the "Tools for Success" section of the Exemplars Library, all users now have access to a folder of lesson resources: slide decks, lesson plans, example student responses, and interactive self-assessment tools that you may use in your own in-person or remote lessons

With students working from home, are you finding it difficult to assess their math understanding and develop a clear picture of their progress? If so, it’s time to switch up your approach to include performance tasks.
Watch our K-2 and 3-5 webinars to explore the Exemplars Problem Solving Procedure and a range of technologies that can keep your students engaged throughout the process.
Teachers need technologies that provide students with a virtual “math playground” to explore, discover, and create. That’s why Exemplars is so excited to be partnering with Brainingcamp! As part of a special offer, Brainingcamp provides free trials and can extend a 15% discount to all Exemplars Math Library subscribers.

Whether your school or district has adopted a remote learning, in-school learning, or a hybrid model this year, Exemplars is pleased to share that it has several new product enhancements and resources to help educators be successful in every environment.
Jay Meadows, Exemplars CEO, speaks with Tina Henckel, Director of STEM Education, K–12 at Norwalk Public Schools about how her district is successfully using Exemplars tasks during this period of remote instruction to enrich math learning.
This online lesson was created by Exemplars enthusiast, Marissa Schlup, from Sioux Falls, SD using the free social learning tool Flipgrid. Her 4th-graders started using Exemplars in February.

Learning with your children at home can be incredibly challenging. What is realistic? What should you expect to accomplish? How should you spend your time?
The Three Reads Protocol is one way to do a close read of a complex math task. This strategy includes reading a math scenario three times with a different goal each time. This blog offers tips and suggestions for how to adapt this method to a virtual learning environment.
Welcome to Exemplars! If you are reading this, you are likely at home hoping to help your child be successful with the math task they have been sent from school. What is an Exemplars task? As a parent, what are you supposed to do to help?
In this tutorial, teachers will learn how to use Kami, a PDF editing and annotating app created specifically for schools, to assign Exemplars tasks to their students. And, students will learn how to use Kami to create digital math solutions to send to their teachers.
Upon completing an Exemplars task, what should a student’s final problem-solving solution look like? In this video, we will walk students through what they should be thinking about and what they should include to create strong math solutions.

This video tutorial is designed specifically for kids to help them get started with our problem-solving process from home.

Your students are working from home–and their learning shouldn't lag. We'll help. How can you continue to engage them with high-quality work that aligns with content that needs to be covered? You can share Exemplars tasks online, and they can share their solutions.

Take a deep breath! Your students do not need to be proficient tomorrow. As with anything new, it’s going to be best to use a model of gradual release as you introduce this to your students. There are several different ways you can approach this …

Paula Smathers has been using Exemplars with her Kindergarten students for 5 years. She shares the steps she takes to make problem solving accessible, engaging, and successful with even the youngest mathematicians.
Our “problem-solving procedure” hits the news in Edutopia — and boosts math and reading scores!

We are pleased to announce that ReContext Data Solutions, LLC, an independent, outside research organization, has determined that Exemplars performance material in mathematics is “evidence-based” and meets ESSA’s Tier 3 standards.

We asked a powerhouse teaching team to share their Exemplars experience. In an inspirational conversation, a panel of educators at Brooklyn's PS 12 offered ten amazing ways that using Exemplars has transformed their school.
“Exemplars changed the way my students look at problems and how they unpack them.” Challenging students with complex multi-step tasks, Problem Solving for the 21st Century: Built for the Common Core gives them a robust framework for developing solutions — so they’re well equipped to tackle such problems on standardized tests.

At The Phoenix School, for many years (first in paper form, now digital) Exemplars has been a vital component of our math program. No more memorization and regurgitation that flies in – and out! — of kids’ brains.
Teachers find the wealth of information included in the Exemplars program to be extremely helpful. We have incorporated Exemplars Summative problems as end-of-topic assessments, and in grades 3–5 we have seen growth of our SBAC scores. We attribute these gains to our work with the Exemplars Problem-Solving Program.
This blog represents part one of a four-part series that explores mathematical connections and offers guidelines, strategies and suggestions for helping teachers elicit this type of thinking from their students. We find many students enjoy making connections once they learn how to reflect and question effectively.

The math laboratory is in its second year at PS 54. Last year, our data saw increased math scores for the classes that participated in the problem-solving lab. This year, the trend continued and all general education students passed the state math exam.
The Exemplars Problem Solving Procedure has supported students in understanding a problem, identifying a strategy to use, solve the problem, communicate findings in words, and trying to solve a problem in another way.

In past years, when attempting to have children write in a mathematics journal, I would read: "This was easy. I like math." My students were not able to successfully reflect or share what they understood about problem solving or mathematics through their writing. Frustrated, I began to read about using math journals in the classroom.
After years of hard work, the Los Alamos school district has become extremely successful in using Exemplars and in, "Making a paradigm shift from focusing on instruction to focusing on student learning and using formative assessment to drive instruction."
According to one student at Tokyo International School (TIS), “Our teachers want us to really understand the mathematics we learn.”

Promoting discourse from rich tasks that move mathematical thinking forward challenges elementary teacher candidates, as their past experiences in working with both mathematics and children is often limited.

Effective use of formative assessment in the classroom is one the most powerful ways to improve student achievement. Research shows that the improvement in performance is dramatic.

From the beginning of the school year, I used Exemplars problem-solving tasks regularly to create routines that have helped my fifth grade students grow and succeed.
This blog represents Part 5 of a five-part series that features a problem-solving task linked to a Math TEKS Unit of Study and a student’s solution in grades K-5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.
This blog represents Part 4 of a five-part series that features a problem-solving task linked to a Math TEKS Unit of Study and a student’s solution in grades K-5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.
This blog represents Part 3 of a five-part series that features a problem-solving task linked to a Math TEKS Unit of Study and a student’s solution in grades K-5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.
This blog represents Part 2 of a five-part series that features a problem-solving task linked to a Unit of Study for the Math TEKS and a student’s solution in grades K–5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.

This blog represents Part 1 of a five-part series that features a problem-solving task linked to a Unit of Study for the Math TEKS and a student’s solution in grades K–5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.

One of the most beneficial features of Exemplars is the ability to differentiate easily for struggling learners. Some need just a little extra support through small group instruction. The more accessible version of Exemplars tasks is perfect for them!
In this post, we’ll look at a fifth grade student’s solution for the task “Seashells for Lydia.” This task is one of a number of Exemplars tasks aligned to the Number and Operations in Base Ten standard 5.NBT.2. It would be given toward the end of the learning time dedicated to this standard.
In this post, we’ll look at a third-grade student’s solution for the task “Bracelets to Sell.” This task is one of a number of Exemplars tasks aligned to the Operations and Algebraic Thinking Standard 3.OA.3. It would be given toward the end of the learning time dedicated to this standard.
In this post, we’ll look at a first-grade student’s solution for the task, “Pictures on the Wall.” This anchor paper demonstrates the criteria for Problem Solving, Reasoning and Proof, Communication, Connections and Representation from the Exemplars assessment rubric.
This blog represents Part 6 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 6 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 5 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 4 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 3 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 3 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 2 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 2 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.
This blog represents Part 1 of a six-part series that features a problem-solving task linked to a CCSS for Mathematical Content and a student’s solution in grades K–5. Evidence of all eight CCSS for Mathematical Practice will be exhibited by the end of the series.

The tasks created by Exemplars are excellent examples of rich problem-solving that naturally elicit the Practice Standards. Below we will look at the Grade 2 task “Barnyard Buddies” and discuss how it meets each of the eight Mathematical Practice Standards as well as content standard 2.OA.A.1.
Jay McTighe and Grant Wiggins have written a “must read” paper in which they offer key ideas to guide the work of transforming the Common Core Standards to a functioning curriculum in a school or district.

Our math scores were the lowest in the county, and our disparity gap was over 30 points. One of the first changes we made was to implement Exemplars. That first year we implemented the program, our math scores increased by over 30 points.
With the new standards and learning expectations outlined in the Common Core, anchor papers can be a useful tool for helping your teachers and students see and understand what meeting the new standards will “look” like in their classrooms.
The Common Core assessment shifts posed challenges for many students. The use of rubrics allow teachers to more easily identify these areas and address them.
To fully implement the Common Core, teachers must have an understanding of what problem solving is, why it is important and how to go about implementing it. For many, the successful teaching of problem solving will require real pedagogical shifts. What do teachers need to know?
Beyond the “bare facts” approach, the use of a well-designed mathematical performance task like those developed by “Exemplars” may reveal how well a student has grasped and applied the math concept in an intervention or lesson(s). The performance task rubric is critical in providing the intervention team with information as to how to help the student continue to increase problem-solving thought patterns.
In mathematics classrooms, teachers must create a “culture of opportunity” where students have the time for and feel free to explore the wonder and beauty of mathematics.
If your school or district is preparing for the integration of the Common Core State Standards (CCSS) into its mathematics curriculum, Exemplars materials are a great bridge.
In this blog, Dr. Julia Watson provides insight on Problem-Based Learning (PBL) and offers suggestions on how teachers might go about incorporating PBL into their classrooms. It is published as a two-part series. The first segment features background information on PBL and its benefits on student learning, while the second will focus on steps for implementation.
In her last post, Dr. Julia Watson provided an overview of Problem-Based Learning (PBL). In this segment, she offers suggestions on how teachers might go about incorporating this approach into their classrooms.
Exemplars standards-based performance tasks provide teachers with not only summative data about their Title I students' progress, but also formative information. As a result, teachers can see what their students know, what they don't know and most importantly where student misconceptions lie so that corrective lessons can be planned.
The Exemplars tasks have proven to be engaging for our Title I students. Use of the student-scoring rubric helps students understand exactly what is expected of them as they solve problems. This knowledge then carries over to other mathematics tasks.
Like the NCTM standards, Exemplars material places a greater emphasis on the "process standards." By focusing on mathematical problem solving and communication, Title I teachers are able to look more closely at what students' work shows about their mathematical understanding.

We saw excellent improvement in students’ understanding of how to break down a problem and model their thinking. I can remember many blank papers in years past when we administered problem-solving tasks. This year we had not one single blank paper! All students were able to find an entry point to begin the task.
Since its opening, Brewer Elementary has struggled with low test scores and student underachievement. But with the help of Exemplars, Brewer Elementary has moved from being a school on the Needs Improvement List to a school named to the Distinguished Schools List. Brewer Elementary is a school-wide Title I site.

From jotting down informal ideas to creating a persuasive formal piece, bringing writing into your science teaching will help your students analyze the concepts further, and can lead to the discovery of new knowledge, connections, and ideas.

Want to help your students develop stronger reading comprehension skills and gain scientific knowledge at the same time? Offering non-fiction science texts in the classroom can do just that!

With the vast amount of literacy and math concepts educators are expected to teach, many of us don’t have as much time for teaching science. But we can find ways to sneak it in. Read on to learn how!

Exemplars Science Consultant, Tracy Lavallee, shares her top 3 read-aloud books for bringing science into the classroom, plus activities to try with them!

How can we get our students genuinely excited about science? It’s a question that so many of us are looking for the answer to. So we’ve started something fun to help: Science Talk!

You’re the chef of your classroom, so feed those hungry minds with our recipe for bringing more science into your teaching.

Kids are natural scientists: driven by curiosity and wonder, always exploring and playing, and always asking questions. They’re already hooked on science—they just may not know it yet! So how do we keep that joyful spark alive in our classrooms?

As schools and districts across the country begin to think about how to re-engage students in learning, consider science as a place to begin. Why science? Because science is naturally engaging for students.

Exemplars understand the constraints on your time. We also know how hard teachers work to provide the best education possible for every student. We want to help you bring more inquiry into your teaching.

Stress has a serious impact on how students learn. Read on to discover some science-based reasons for making fun a priority, and how to do it without losing sight of your curricular goals.

Long gone are the days of the stand and deliver as an effective way to teach. Science instruction is now more about sense-making than memorization.

Time. It seems we never have enough time. Not enough time to teach everything we need to teach. And science is usually the subject most affected by this lack of time.

If our children understand the why and the how of science, technology, and engineering, they are better able to make informed decisions as part of a democratic society. In order for students to do this, they must regularly engage with, investigate, and explain scientific phenomena.
Science is rich with opportunities for communication. In fact, a large part of science involves students talking, writing and reading. This communication may include scientists' meetings to discuss ideas and investigations, science journals to record observations and data, or the use of trade books to help illustrate concepts.

This blog features a few suggestions for getting started with Exemplars Science. There is no right or wrong way to begin. The important thing is to begin. Have fun with it!

Math Exemplars work to develop the whole child in mathematics and social-emotional learning.

It is a new year with new students and new problems to solve! There is nothing like having the opportunity to start the year off fresh. My number one goal in the very beginning is to help students fall in love with solving problems.

When you walk into my classroom, you might be taken aback by the noise level. But don't worry, it's intentional.

Encouraging students to work together can lead to deeper understanding for all students, and in turn boost mathematical achievement.

This new mathematical formula interconnects Exemplars problem-solving tasks and the CASEL framework. The agendas of both the CASEL and Exemplars pedagogies strive to create classroom cultures that are heavily student-focused and driven by personal growth.

In order to support a talk rich classroom, I need to feed the learning. The Exemplars problems are rich and engaging tasks that my students eagerly unpack. With each new unit of study, I follow an instructional routine that allows students to acquire knowledge and skills in a predictable manner.

Exemplars tasks provide a welcome contrast to the school district’s highly-structured and scripted base math program. It is through the Exemplars tasks that my students are freed to use their creativity and find their voices as young mathematicians
“Exemplars changed the way my students look at problems and how they unpack them.” Challenging students with complex multi-step tasks, Problem Solving for the 21st Century: Built for the Common Core gives them a robust framework for developing solutions — so they’re well equipped to tackle such problems on standardized tests.

At The Phoenix School, for many years (first in paper form, now digital) Exemplars has been a vital component of our math program. No more memorization and regurgitation that flies in – and out! — of kids’ brains.

Teachers find the wealth of information included in the Exemplars program to be extremely helpful. We have incorporated Exemplars Summative problems as end-of-topic assessments, and in grades 3–5 we have seen growth of our SBAC scores. We attribute these gains to our work with the Exemplars Problem-Solving Program.

The math laboratory is in its second year at PS 54. Last year, our data saw increased math scores for the classes that participated in the problem-solving lab. This year, the trend continued and all general education students passed the state math exam.
The Exemplars Problem Solving Procedure has supported students in understanding a problem, identifying a strategy to use, solve the problem, communicate findings in words, and trying to solve a problem in another way.
Science is rich with opportunities for communication. In fact, a large part of science involves students talking, writing and reading. This communication may include scientists' meetings to discuss ideas and investigations, science journals to record observations and data, or the use of trade books to help illustrate concepts.

In past years, when attempting to have children write in a mathematics journal, I would read: "This was easy. I like math." My students were not able to successfully reflect or share what they understood about problem solving or mathematics through their writing. Frustrated, I began to read about using math journals in the classroom.
After years of hard work, the Los Alamos school district has become extremely successful in using Exemplars and in, "Making a paradigm shift from focusing on instruction to focusing on student learning and using formative assessment to drive instruction."
According to one student at Tokyo International School (TIS), “Our teachers want us to really understand the mathematics we learn.”

Promoting discourse from rich tasks that move mathematical thinking forward challenges elementary teacher candidates, as their past experiences in working with both mathematics and children is often limited.

From the beginning of the school year, I used Exemplars problem-solving tasks regularly to create routines that have helped my fifth grade students grow and succeed.

One of the most beneficial features of Exemplars is the ability to differentiate easily for struggling learners. Some need just a little extra support through small group instruction. The more accessible version of Exemplars tasks is perfect for them!

The tasks created by Exemplars are excellent examples of rich problem-solving that naturally elicit the Practice Standards. Below we will look at the Grade 2 task “Barnyard Buddies” and discuss how it meets each of the eight Mathematical Practice Standards as well as content standard 2.OA.A.1.

Our math scores were the lowest in the county, and our disparity gap was over 30 points. One of the first changes we made was to implement Exemplars. That first year we implemented the program, our math scores increased by over 30 points.
With the new standards and learning expectations outlined in the Common Core, anchor papers can be a useful tool for helping your teachers and students see and understand what meeting the new standards will “look” like in their classrooms.
Beyond the “bare facts” approach, the use of a well-designed mathematical performance task like those developed by “Exemplars” may reveal how well a student has grasped and applied the math concept in an intervention or lesson(s). The performance task rubric is critical in providing the intervention team with information as to how to help the student continue to increase problem-solving thought patterns.
When teachers consider lesson planning, they typically think of the assessments last. This is natural, because the end of a unit of study typically culminates with the “big test,” or “final exam.” This misconception, however, causes inefficient and ineffective instruction.
In this blog, Dr. Julia Watson provides insight on Problem-Based Learning (PBL) and offers suggestions on how teachers might go about incorporating PBL into their classrooms. It is published as a two-part series. The first segment features background information on PBL and its benefits on student learning, while the second will focus on steps for implementation.
In her last post, Dr. Julia Watson provided an overview of Problem-Based Learning (PBL). In this segment, she offers suggestions on how teachers might go about incorporating this approach into their classrooms.
Exemplars standards-based performance tasks provide teachers with not only summative data about their Title I students' progress, but also formative information. As a result, teachers can see what their students know, what they don't know and most importantly where student misconceptions lie so that corrective lessons can be planned.
The Exemplars tasks have proven to be engaging for our Title I students. Use of the student-scoring rubric helps students understand exactly what is expected of them as they solve problems. This knowledge then carries over to other mathematics tasks.
Like the NCTM standards, Exemplars material places a greater emphasis on the "process standards." By focusing on mathematical problem solving and communication, Title I teachers are able to look more closely at what students' work shows about their mathematical understanding.

We saw excellent improvement in students’ understanding of how to break down a problem and model their thinking. I can remember many blank papers in years past when we administered problem-solving tasks. This year we had not one single blank paper! All students were able to find an entry point to begin the task.
Since its opening, Brewer Elementary has struggled with low test scores and student underachievement. But with the help of Exemplars, Brewer Elementary has moved from being a school on the Needs Improvement List to a school named to the Distinguished Schools List. Brewer Elementary is a school-wide Title I site.

Dr. Brewer, founder of Exemplars, along with others, asked an important question, “How do we determine if students can utilize the mathematics they are learning in the classroom to address and solve the complex problems they eventually will be asked to address in the “real world?”

We're highlighted in Edutopia again—this time for how well our authentic tasks promote productive math struggle.

We're kicking off 5 Days of Exemplars, a series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. You’ll discover new ideas you can use right away!

How do we prepare our students for end-of-year performance tasks on statewide tests while—at the same time—ensure that we are utilizing the precious minutes in every class period and are not “teaching to the tests?”

Exemplars understand the constraints on your time. We also know how hard teachers work to provide the best education possible for every student. We want to help you bring more inquiry into your teaching.

After 13 years in education, I have used Exemplars in different grade levels and various demographic and socioeconomic areas, but the results were always the same. The real-life connections, self-motivation to gain the desired level, and the critical higher-order reasoning that is expected both challenges and motivates all types of students.

Students enjoy thinking for themselves—they need your support, but not too much! So how do you offer just the right guidance and ask just enough questions without inadvertently “stealing” their opportunity to solve the problem on their own and the thrill of discovery that will keep them engaged through a challenge?

Once you've prepared your students with a solid understanding of complex performance tasks ... and once you've guided them as s they select a strategy for solving it ... what's your role–and what's your goal–as they work to find solutions? Check out these best practices.
Your students can find an answer. But can they create solutions? The difference between a simple answer–a simple computation, for example–and a rich mathematical solution that demonstrates the depth of their understanding is vast. Learn about a simple framework that supports students in developing persuasive solutions.
When students assess their own work at the end of a task they not only discover how to improve their solutions, but they build skills that will empower them throughout their problem-solving lives. Learn how to apply self- and peer-assessment practices in your classroom to boost key critical thinking and reasoning skills.

We’re sharing 5 Days of Exemplars, a blog series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. Read on to learn more.
Teachers need technologies that provide students with a virtual “math playground” to explore, discover, and create. That’s why Exemplars is so excited to be partnering with Brainingcamp! As part of a special offer, Brainingcamp provides free trials and can extend a 15% discount to all Exemplars Math Library subscribers.
The Three Reads Protocol is one way to do a close read of a complex math task. This strategy includes reading a math scenario three times with a different goal each time. This blog offers tips and suggestions for how to adapt this method to a virtual learning environment.
Welcome to Exemplars! If you are reading this, you are likely at home hoping to help your child be successful with the math task they have been sent from school. What is an Exemplars task? As a parent, what are you supposed to do to help?
In this tutorial, teachers will learn how to use Kami, a PDF editing and annotating app created specifically for schools, to assign Exemplars tasks to their students. And, students will learn how to use Kami to create digital math solutions to send to their teachers.
Upon completing an Exemplars task, what should a student’s final problem-solving solution look like? In this video, we will walk students through what they should be thinking about and what they should include to create strong math solutions.

This video tutorial is designed specifically for kids to help them get started with our problem-solving process from home.

Your students are working from home–and their learning shouldn't lag. We'll help. How can you continue to engage them with high-quality work that aligns with content that needs to be covered? You can share Exemplars tasks online, and they can share their solutions.
This blog represents part one of a four-part series that explores mathematical connections and offers guidelines, strategies and suggestions for helping teachers elicit this type of thinking from their students. We find many students enjoy making connections once they learn how to reflect and question effectively.

Long gone are the days of the stand and deliver as an effective way to teach. Science instruction is now more about sense-making than memorization.

Time. It seems we never have enough time. Not enough time to teach everything we need to teach. And science is usually the subject most affected by this lack of time.
Science is rich with opportunities for communication. In fact, a large part of science involves students talking, writing and reading. This communication may include scientists' meetings to discuss ideas and investigations, science journals to record observations and data, or the use of trade books to help illustrate concepts.

Effective use of formative assessment in the classroom is one the most powerful ways to improve student achievement. Research shows that the improvement in performance is dramatic.

As you begin preparing your staff to focus on the new math TEKS this year, rubrics should play a key role in terms of helping your teachers and students achieve success with the new standards.

Problem solving is a life-long skill all mathematicians use. The true power of a mathematician is the ability to see math in all situations and solve problems using a toolbox of proven strategies.
Prior to 2006, many states—including Texas—had a math curriculum that was perceived to be “an inch deep and a mile wide.” Teachers were required to teach a large number of math skills that spiraled from grade to grade and seemed both disconnected and fragmented.
Once upon a time, Americans might have been content to live in a community much like Garrison Keillor’s Lake Wobegon, “where all the children are above average.” That’s because historically American kids, and our schools, were above average; however, for decades, America’s education system has been losing ground internationally.
With the new standards and learning expectations outlined in the Common Core, anchor papers can be a useful tool for helping your teachers and students see and understand what meeting the new standards will “look” like in their classrooms.
The Common Core assessment shifts posed challenges for many students. The use of rubrics allow teachers to more easily identify these areas and address them.
To fully implement the Common Core, teachers must have an understanding of what problem solving is, why it is important and how to go about implementing it. For many, the successful teaching of problem solving will require real pedagogical shifts. What do teachers need to know?
Beyond the “bare facts” approach, the use of a well-designed mathematical performance task like those developed by “Exemplars” may reveal how well a student has grasped and applied the math concept in an intervention or lesson(s). The performance task rubric is critical in providing the intervention team with information as to how to help the student continue to increase problem-solving thought patterns.
If your school or district is preparing for the integration of the Common Core State Standards (CCSS) into its mathematics curriculum, Exemplars materials are a great bridge.

This blog features a few suggestions for getting started with Exemplars Science. There is no right or wrong way to begin. The important thing is to begin. Have fun with it!

Once upon a time, Americans might have been content to live in a community much like Garrison Keillor’s Lake Wobegon, “where all the children are above average.” That’s because historically American kids, and our schools, were above average; however, for decades, America’s education system has been losing ground internationally.

We're highlighted in Edutopia again—this time for how well our authentic tasks promote productive math struggle.

To help your students achieve indelible long-term learning, let’s use the latest in brain research to their advantage.
Our “problem-solving procedure” hits the news in Edutopia — and boosts math and reading scores!

We are pleased to announce that ReContext Data Solutions, LLC, an independent, outside research organization, has determined that Exemplars performance material in mathematics is “evidence-based” and meets ESSA’s Tier 3 standards.
ReContext Data Solutions, LLC, an independent, outside research organization, has determined that Exemplars materials and pedagogy is "evidence-based" and meets ESSA's Tier 4 standards.

Effective use of formative assessment in the classroom is one the most powerful ways to improve student achievement. Research shows that the improvement in performance is dramatic.
To fully implement the Common Core, teachers must have an understanding of what problem solving is, why it is important and how to go about implementing it. For many, the successful teaching of problem solving will require real pedagogical shifts. What do teachers need to know?

Once upon a time, Americans might have been content to live in a community much like Garrison Keillor’s Lake Wobegon, “where all the children are above average.” That’s because historically American kids, and our schools, were above average; however, for decades, America’s education system has been losing ground internationally.

We're kicking off 5 Days of Exemplars, a series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. You’ll discover new ideas you can use right away!

Our kids have been learning—because that’s what teachers do. They get kids to learn, no matter what. And this year, they made magic.

Exemplars tasks provide a welcome contrast to the school district’s highly-structured and scripted base math program. It is through the Exemplars tasks that my students are freed to use their creativity and find their voices as young mathematicians
This is the start of a strong solution. Welcome to day one of our deep dive into how to help students grow into capable, confident problem solvers. For students to realize the full benefits of authentic problem-solving tasks, you need strategies to help them successfully read and unpack these rigorous problems. Read on for effective strategies.

Students enjoy thinking for themselves—they need your support, but not too much! So how do you offer just the right guidance and ask just enough questions without inadvertently “stealing” their opportunity to solve the problem on their own and the thrill of discovery that will keep them engaged through a challenge?

Once you've prepared your students with a solid understanding of complex performance tasks ... and once you've guided them as s they select a strategy for solving it ... what's your role–and what's your goal–as they work to find solutions? Check out these best practices.
Your students can find an answer. But can they create solutions? The difference between a simple answer–a simple computation, for example–and a rich mathematical solution that demonstrates the depth of their understanding is vast. Learn about a simple framework that supports students in developing persuasive solutions.
When students assess their own work at the end of a task they not only discover how to improve their solutions, but they build skills that will empower them throughout their problem-solving lives. Learn how to apply self- and peer-assessment practices in your classroom to boost key critical thinking and reasoning skills.

We’re sharing 5 Days of Exemplars, a blog series that will share new ideas and established best practices for getting your students engaged and energized in problem solving. Read on to learn more.
In the "Tools for Success" section of the Exemplars Library, all users now have access to a folder of lesson resources: slide decks, lesson plans, example student responses, and interactive self-assessment tools that you may use in your own in-person or remote lessons

With students working from home, are you finding it difficult to assess their math understanding and develop a clear picture of their progress? If so, it’s time to switch up your approach to include performance tasks.
Watch our K-2 and 3-5 webinars to explore the Exemplars Problem Solving Procedure and a range of technologies that can keep your students engaged throughout the process.
Teachers need technologies that provide students with a virtual “math playground” to explore, discover, and create. That’s why Exemplars is so excited to be partnering with Brainingcamp! As part of a special offer, Brainingcamp provides free trials and can extend a 15% discount to all Exemplars Math Library subscribers.
Jay Meadows, Exemplars CEO, speaks with Tina Henckel, Director of STEM Education, K–12 at Norwalk Public Schools about how her district is successfully using Exemplars tasks during this period of remote instruction to enrich math learning.
This online lesson was created by Exemplars enthusiast, Marissa Schlup, from Sioux Falls, SD using the free social learning tool Flipgrid. Her 4th-graders started using Exemplars in February.

Learning with your children at home can be incredibly challenging. What is realistic? What should you expect to accomplish? How should you spend your time?
The Three Reads Protocol is one way to do a close read of a complex math task. This strategy includes reading a math scenario three times with a different goal each time. This blog offers tips and suggestions for how to adapt this method to a virtual learning environment.
Welcome to Exemplars! If you are reading this, you are likely at home hoping to help your child be successful with the math task they have been sent from school. What is an Exemplars task? As a parent, what are you supposed to do to help?
In this tutorial, teachers will learn how to use Kami, a PDF editing and annotating app created specifically for schools, to assign Exemplars tasks to their students. And, students will learn how to use Kami to create digital math solutions to send to their teachers.
Upon completing an Exemplars task, what should a student’s final problem-solving solution look like? In this video, we will walk students through what they should be thinking about and what they should include to create strong math solutions.

This video tutorial is designed specifically for kids to help them get started with our problem-solving process from home.

Your students are working from home–and their learning shouldn't lag. We'll help. How can you continue to engage them with high-quality work that aligns with content that needs to be covered? You can share Exemplars tasks online, and they can share their solutions.

