Understanding Mathematical Connections at the First Grade Level
Written By: Deborah Armitage, M.Ed., Exemplars Math Consultant
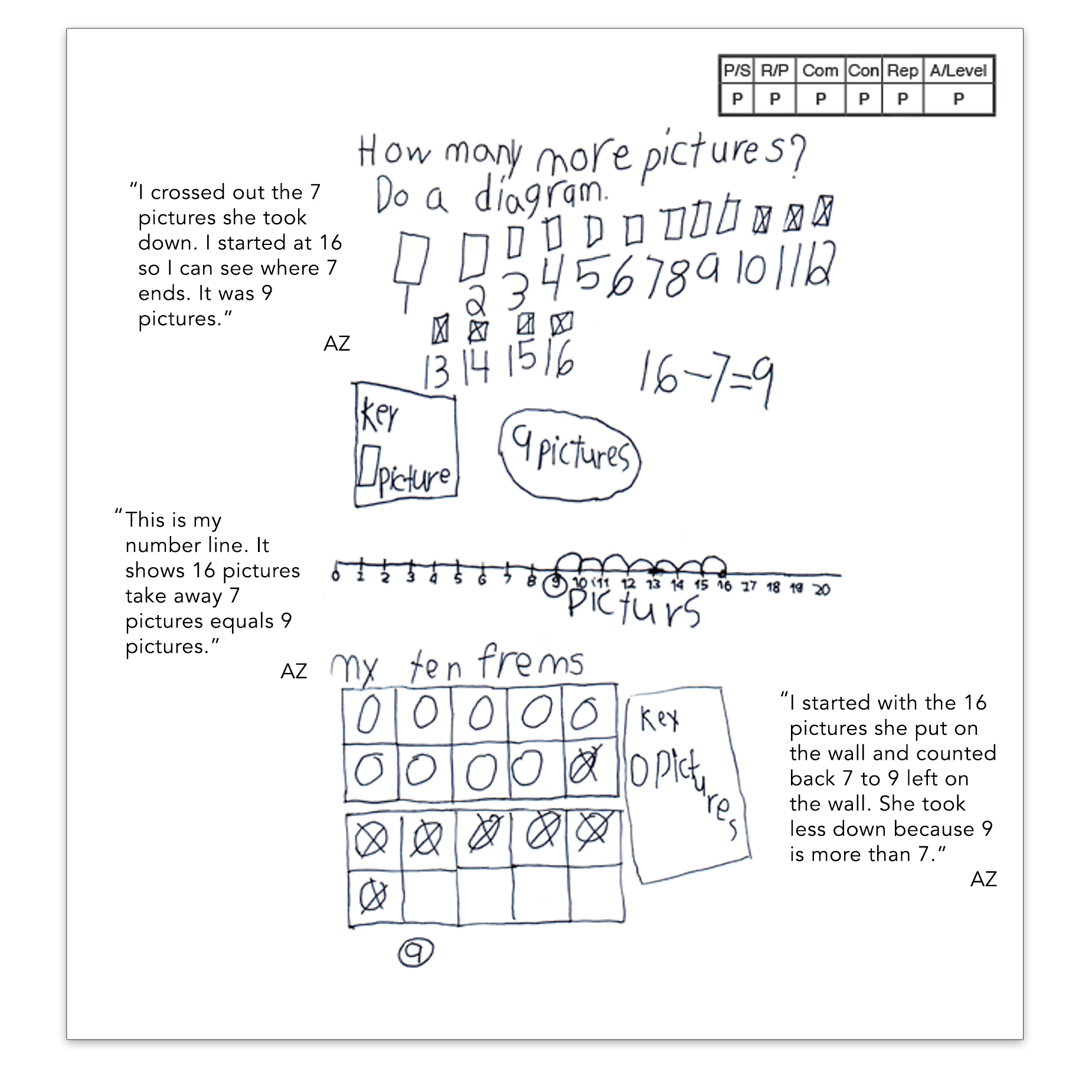
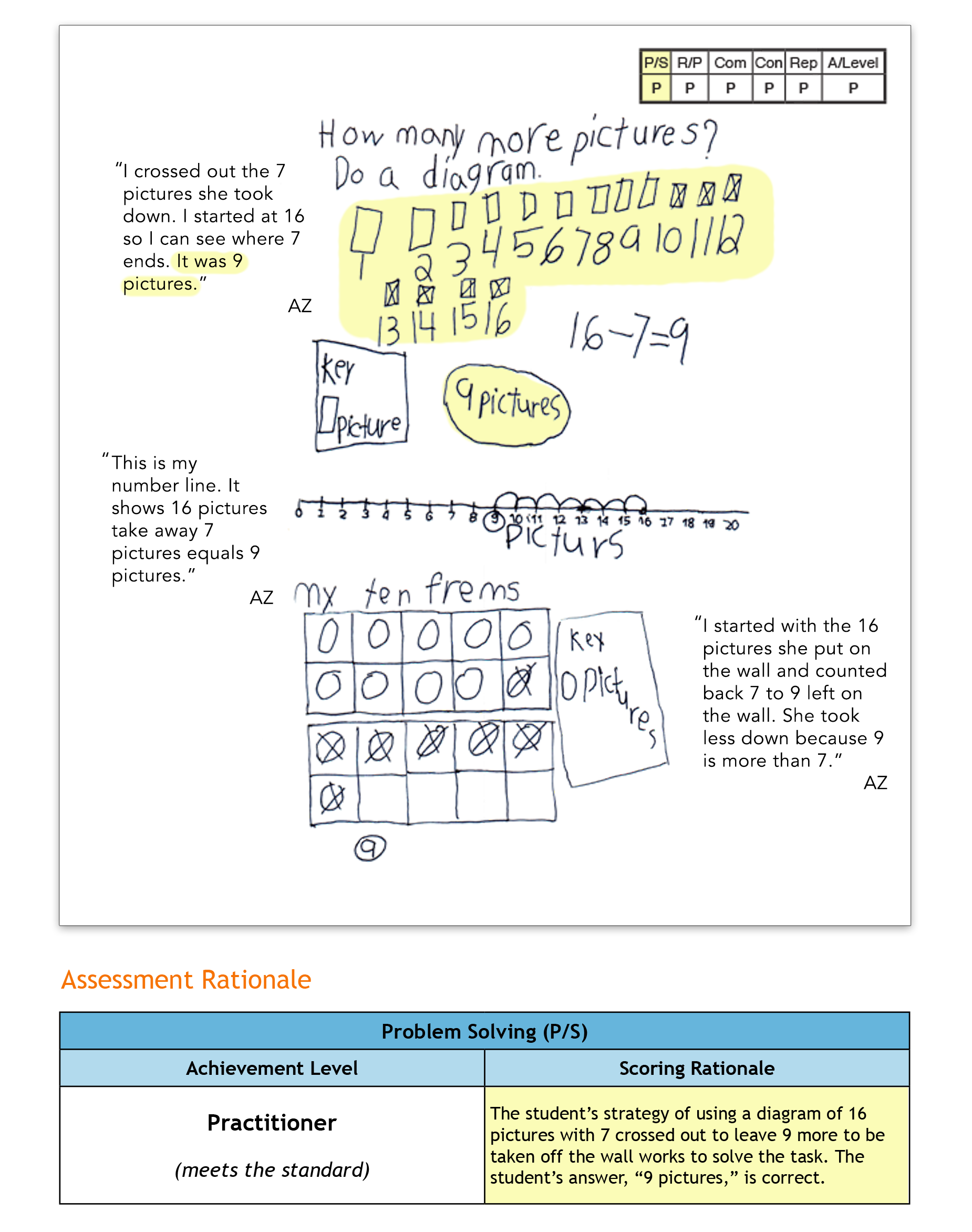
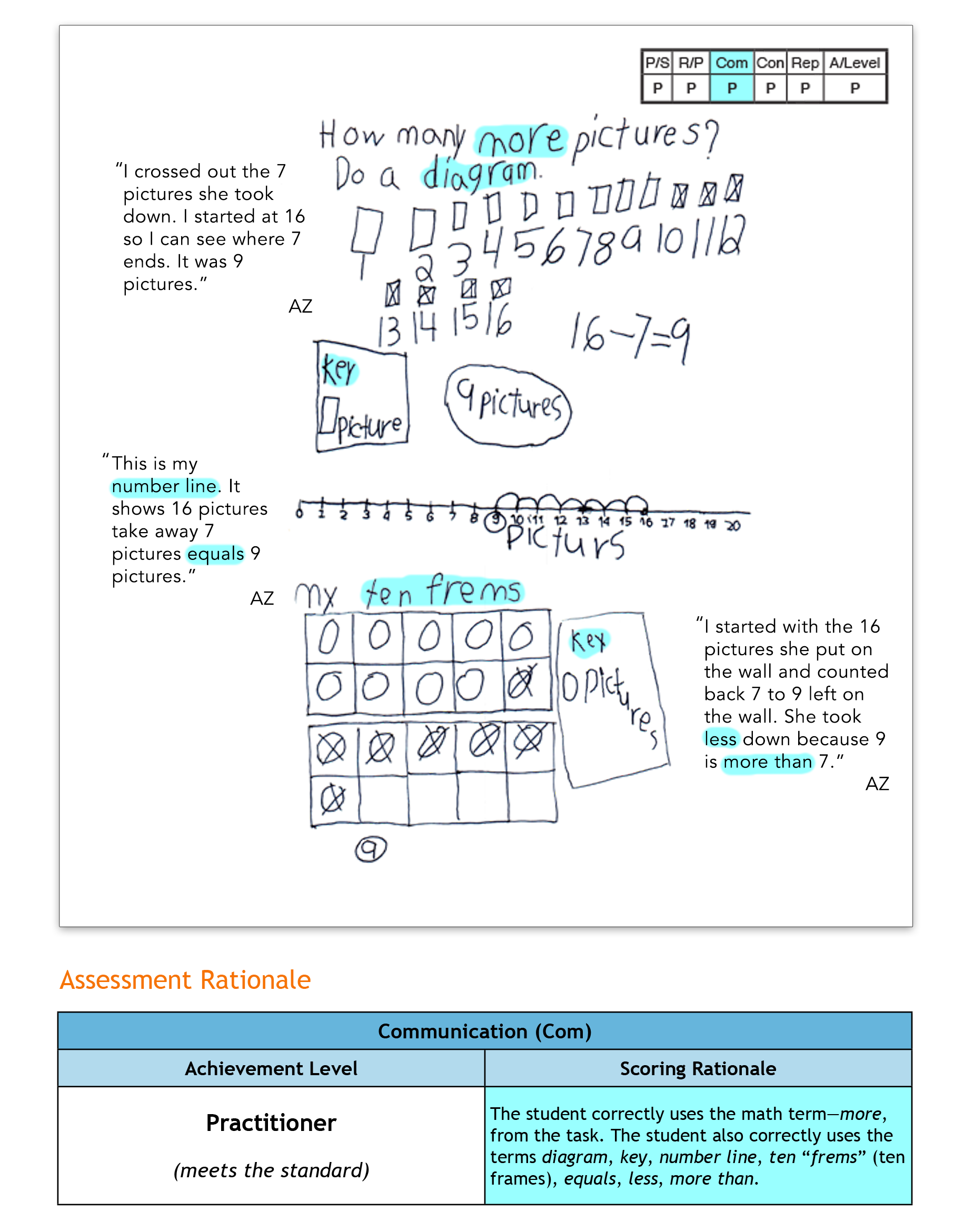
In today’s post, we’ll look at a first-grade student’s solution for the task, “Pictures on the Wall.” This anchor paper demonstrates the criteria for Problem Solving, Reasoning and Proof, Communication, Connections and Representation from the Exemplars assessment rubric. It also shows a solution that goes beyond arithmetic calculation and provides the evidence that a student can reflect on and apply mathematical connections. The beauty of mathematical connections is that they often begin with the other four rubric criteria. In other words, the Exemplars rubric provides multiple opportunities for a student to connect mathematically!
In this piece of student work, you’ll also notice that the teacher has “scribed” the student’s oral explanation. Scribing allows teachers to fully capture the mathematical reasoning of early writers.
This blog will offer tips for the type of instructional support a teacher may provide during this learning time as well as the type of support students may give each other. Teacher support may range from offering direct instruction to determining if a student independently included mathematical connections in her or his solution. After reading this post, give the task a try in your own classroom along with the Exemplars rubric. You may view other Exemplars tasks here.
First Grade Task: Pictures on the Wall
There are sixteen pictures on a wall. The art teacher wants to take all the pictures off the wall to put up new pictures. The art teacher takes seven pictures off the wall. How many more pictures does the art teacher have to take off the wall? Show all your mathematical thinking.
Common Core Alignments
- Content Standard 1.OA.6: Add and subtract within 20, demonstrating fluency for addition and subtraction within 10. Use strategies such as counting on; making ten (e.g., 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decomposing a number leading to a ten (e.g., 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); using the relationship between addition and subtraction (e.g., knowing that 8 + 4 = 12, one knows 12 – 8 = 4); and creating equivalent but easier or known sums (e.g., adding 6 + 7 by creating the known equivalent 6 + 6 + 1 = 12 + 1 = 13).
- Mathematical Practices: MP1, MP3, MP4, MP5, MP6
Click on the orange arrow to the right of the solution below to view Exemplars scoring rationales.