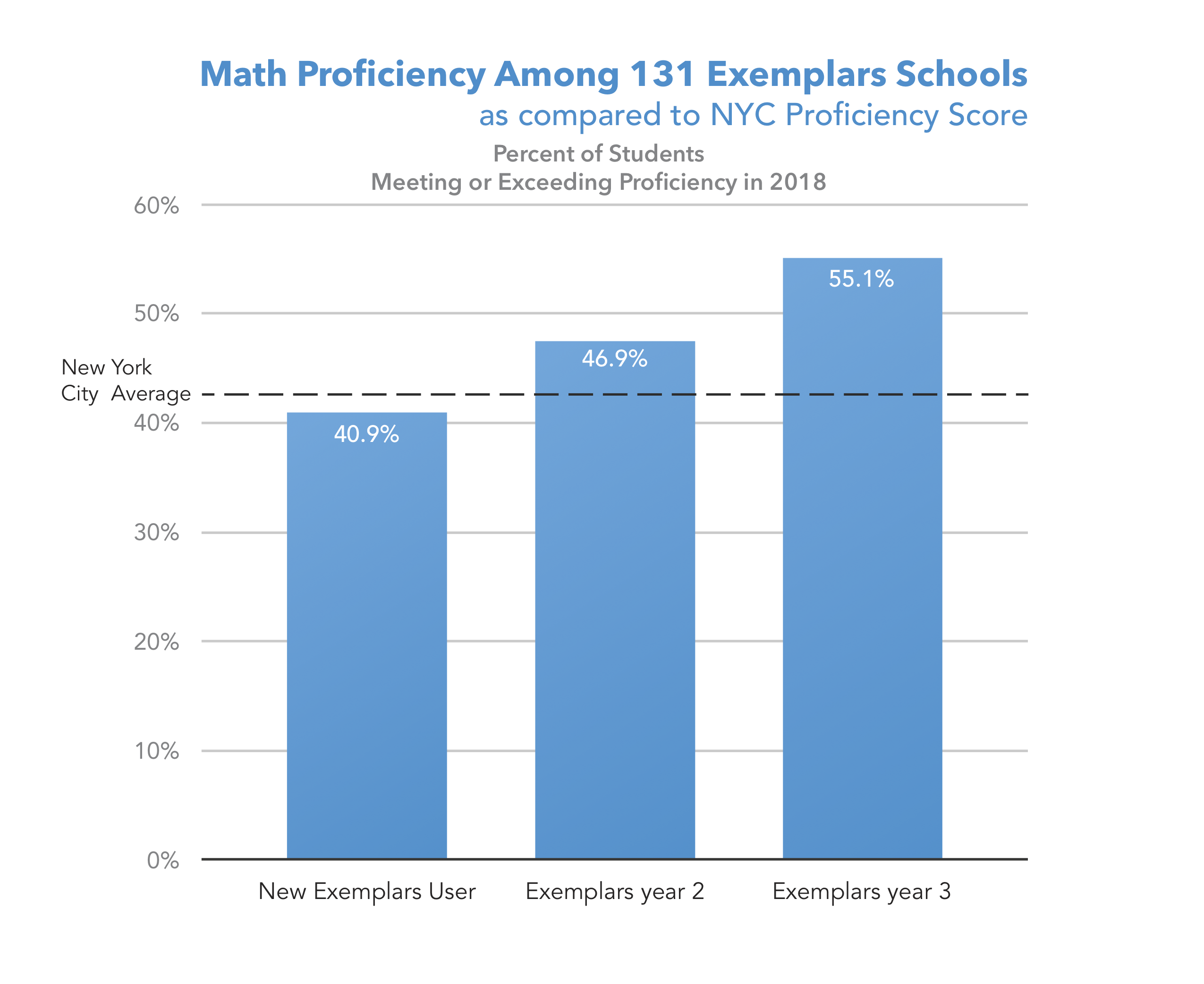
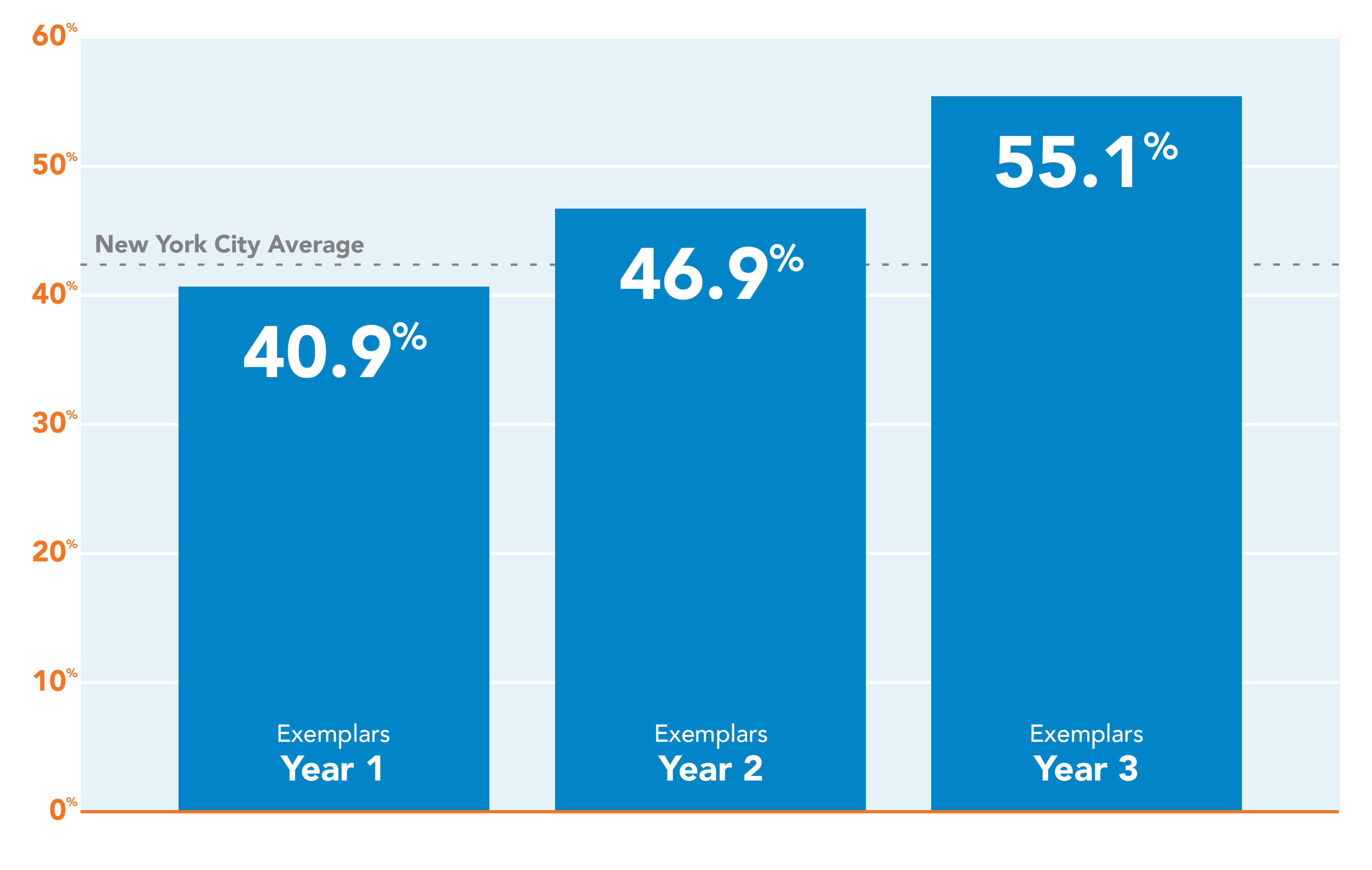
Better Learning Outcomes With Exemplars
What Educators Are Saying
Find us in:
Getting Stuck in Math and Coming Out Stronger
Edutopia highlights Exemplars as a “go-to” for promoting productive math struggle.
The Top 3 Things My Students Love About Exemplars
Why are the students so happy? I really wanted to know. So, I did what anyone would do: I went straight to the source and asked the kiddos. Here’s what I learned.
Grow Student Confidence Through Problem Solving
Math Exemplars work to develop the whole child in mathematics and social-emotional learning.