Supporting the TEKS Mathematical Processes with Exemplars Performance Tasks and Rubric at the Fourth Grade Level
Written By Exemplars Math Consultants: Deborah Armitage, M.Ed. and Dinah Chancellor, M.Ed.
Summer Blog Series Overview:
Exemplars performance-based material is a supplemental resource that provides teachers with an effective way to implement the Math TEKS through problem solving. This blog represents Part 5 of a five-part series that features a problem-solving task linked to a Math TEKS Unit of Study and a student’s solution in grades K-5. Evidence of all seven Mathematical Process Standards will be exhibited by the end of the series.
The Exemplars Standards-Based Math Rubric allows teachers to examine student work against a set of analytic criteria that consists of the following categories: Problem Solving, Reasoning and Proof, Communication, Connections and Representation. There are four performance/achievement levels: Novice, Apprentice, Practitioner (meets the standard) and Expert. The Novice and Apprentice levels support a student’s progress toward being able to apply the criteria of a Practitioner and Expert. It is at these higher levels of achievement where support for the Mathematical Processes is found.
Exemplars problem-solving tasks provide students with an opportunity to apply their conceptual understanding of standards, mathematical processes and skills. Observing student anchor papers with assessment rationales that demonstrate the alignment between the Exemplars assessment rubric and the Math TEKS can be insightful for educators. Anchor papers and assessment rationales provide examples of what to look for in your own students’ work. Examples of Exemplars rubric criteria and the Mathematical Processes are embedded in the assessment rationales at the bottom of the page. The full version of our rubric may be accessed here. It is often helpful to have this in hand while reviewing a piece of student work.
Blog 4: Observations at the Fourth Grade Level
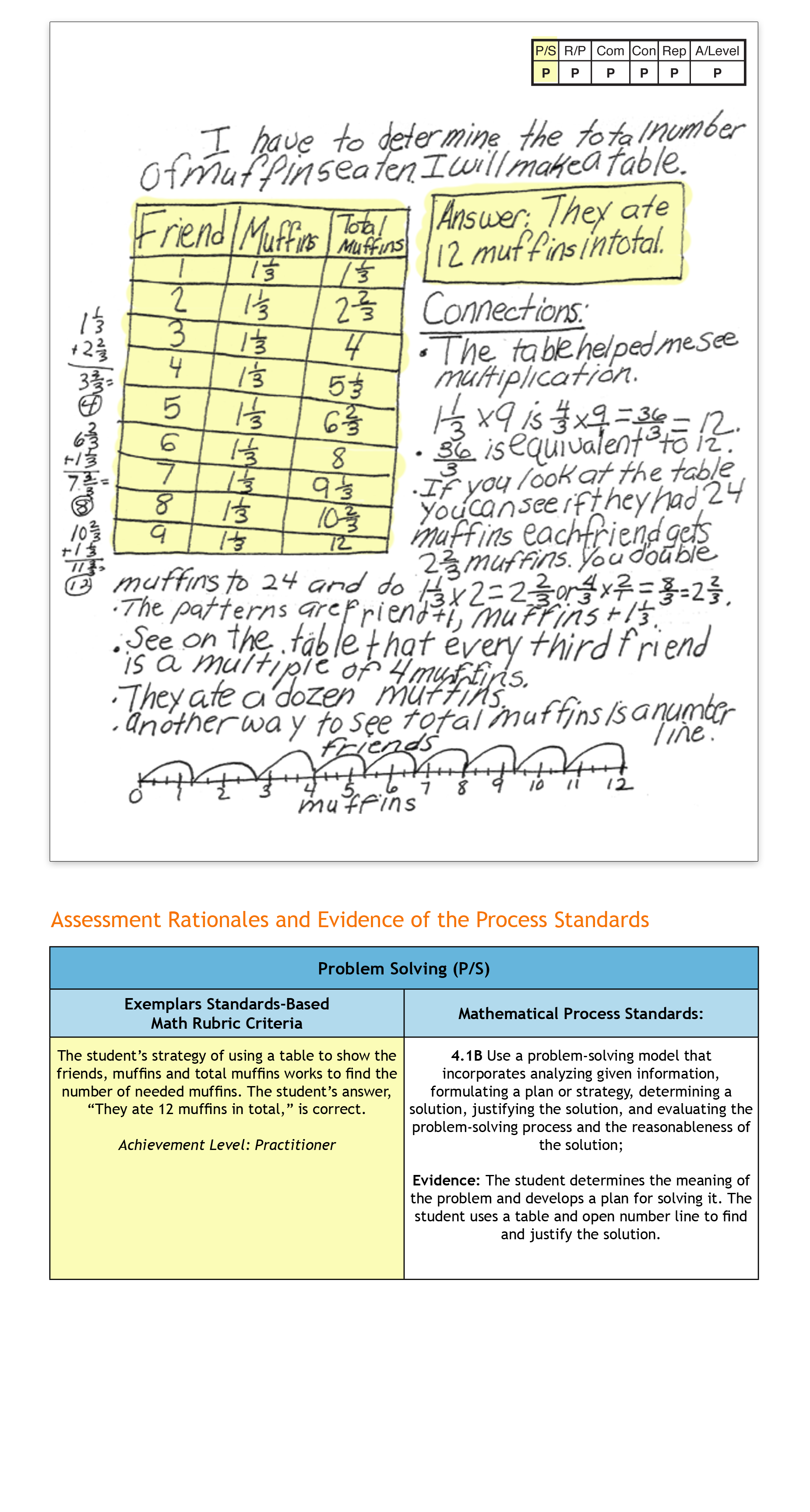
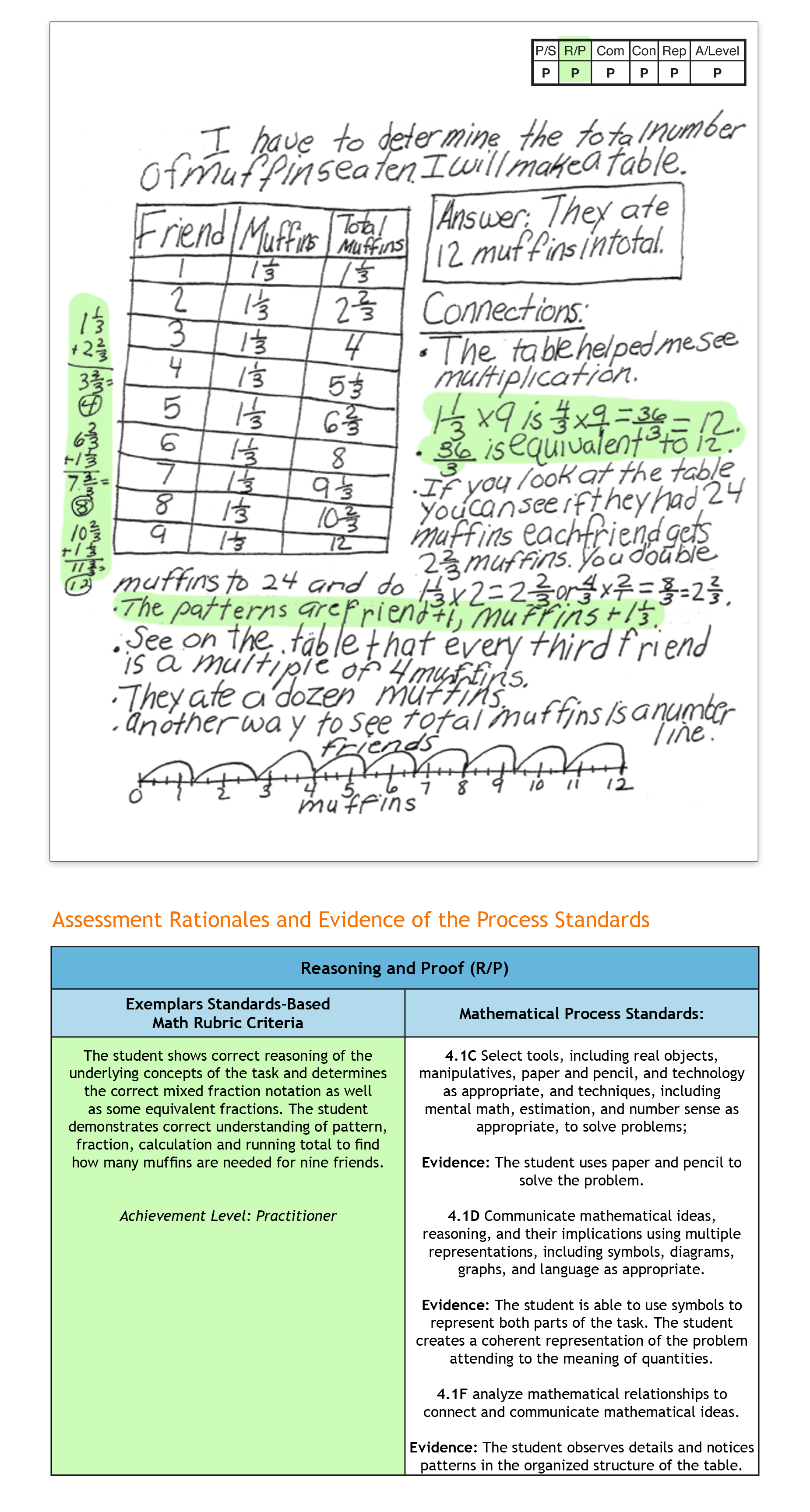
The fifth anchor paper and set of rationales we’ll review in this series is taken from a fourth grade student’s solution for the task “Sharing Muffins.” This task is one of a number of Exemplars tasks aligned to the Adding and Subtracting Fractions Unit.
“Sharing Muffins” could be used toward the end of the learning time allocated to this Unit. This task provides fourth graders with an opportunity to apply different strategies to determine the number of muffins needed for each of nine friends to have one and one-third muffins. In solving this task, there are a variety of strategies for students to consider. Some examples include using actual muffins to model one and one-third muffins per friend or diagramming the muffins using a table, tally chart or number line. In their solutions, students may replace each mixed number with an equivalent fraction. Addition, subtraction and multiplication of fractions may also be used.
Fourth Grade Task: Sharing Muffins
Nine friends are going to equally share some muffins. Each muffin is the same size. Each friend gets one and one-third muffins. How many muffins did the nine friends equally share? Show all your mathematical thinking.
Math TEKS Alignments:
Adding and Subtracting Fractions Unit
The Adding and Subtracting Fractions Unit involves using a variety of methods to join or separate parts referring to the same whole. Methods may include replacing mixed numbers with equivalent fractions; using properties of operations and the relationship between addition and subtraction; and using visual models of fractions. Questions to answer may include:
- Why must we use the same “whole” when adding or subtracting fractional parts?
- How can a number line represent adding or subtracting fractions?
- How can benchmark fractions help to determine whether a sum or difference makes sense?
The standards covered in this Unit include:
4.3 Number & operations. The student applies mathematical process standards to represent and generate fractions to solve problems. The student is expected to:
- 4.3A represent a fraction a/b as a sum of fractions 1/b, where a and b are whole numbers and b > 0, including when a > b.
- 4.3B decompose a fraction in more than one way into a sum of fractions with the same denominator using concrete and pictorial models and recording results with symbolic representations such as 7/8 = 5/8 + 2/8; 7/8 = 3/8 + 4/8; 2 7/8 = 1 + 1 + 7/8; 2 7/8 = 8/8 + 8/8 + 7/8;
- 4.3E represent and solve addition and subtraction of fractions with equal denominators using objects and pictorial models that build to the number line and properties of operations;
- 4.3F evaluate the reasonableness of sums and differences of fractions using benchmark fractions 0, 1/4, 1/2, 3/4, and 1, referring to the same whole.
Mathematical Process Standards
The student uses mathematical processes to acquire and demonstrate mathematical understanding. The student is expected to:
- 4.1A apply mathematics to problems arising in everyday life, society, and the workplace;
- 4.1B use a problem-solving model that incorporates analyzing given information, formulating a plan or strategy, determining a solution, justifying the solution, and evaluating the problem-solving process and the reasonableness of the solution;
- 4.1C select tools, including real objects, manipulatives, paper and pencil, and technology as appropriate, and techniques, including mental math, estimation, and number sense as appropriate, to solve problems;
- 4.1E create and use representations to organize, record, and communicate mathematical ideas;
- 4.1F analyze mathematical relationships to connect and communicate mathematical ideas; and
- 4.1G display, explain, and justify mathematical ideas and arguments using precise mathematical language in written or oral communication.